[프로그래머스] 2개 이하로 다른 비트, 비트 시프트 연산자, 비트 XOR

https://school.programmers.co.kr/learn/courses/30/lessons/77885

프로그래머스

문제 설명

양의 정수 x에 대한 함수 f(x)를 다음과 같이 정의합니다.

• x보다 크고 x와 비트가 1~2개 다른 수들 중에서 제일 작은 수

예를 들어,

• f(2) = 3 입니다. 다음 표와 같이 2보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 3이기 때문입니다.

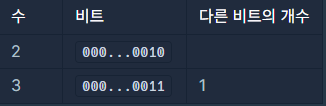
• f(7) = 11 입니다. 다음 표와 같이 7보다 큰 수들 중에서 비트가 다른 지점이 2개 이하이면서 제일 작은 수가 11이기 때문입니다.

정수들이 담긴 배열 numbers가 매개변수로 주어집니다. 

numbers의 모든 수들에 대하여 각 수의 f 값을 배열에 차례대로 담아 return 하도록 solution 함수를 완성해주세요.

---

제한 사항

• 1 ≤ numbers의 길이 ≤ 100,000
• 0 ≤ numbers의 모든 수 ≤ 10**15

---

풀이

문제를 풀기위해 가설을 세워보자.

• 이진법의 가장 오른쪽부터 1이 어디까지 있는지를 확인
• 가장 오른쪽에 1이 있다면 1이 연속되는지 확인, 연속되는 1중 가장 왼쪽의 1을 찾은 후 비트이동
• 가장 오른쪽에 1이 없다면 1추가

몇가지 예를 들면,

위 가설이 맞는것을 알 수 있다.

 

로직

• 가장 오른쪽 비트가 1인지 확인
• 맞다면 bit_cnt += 1 하고 반복
• bit_cnt가 1이상이면 비트가 다른 가장 작은 다음 숫자는 + 2 ** ( bit_cnt  - 1)
• bit_cnt가 0이면 비트가 다른 가장 작은 다음 숫자는 + 1

 

초기 코드

# 초기 코드
def solution(numbers):
    answer = []
    for i in numbers:
        num = i
        cnt = 0
        while i % 2 == 1:
            cnt += 1
            i //= 2
        answer.append(num + 2**(cnt - 1) if cnt != 0 else num + 1)
    return answer
# 440.17ms, 25.3MB

위에 있는 로직을 바로 나타낸 코드이다.

사실 여기서 더 줄일게 있을까해서 찾아보니 비트 시프트 연산자를 활용해서 문제를 푼 사람이 있었다.

 

인상 깊은 풀이 : 비트 시프트 연산자, 비트 XOR

# 인상 깊은 풀이
def solution(numbers):
    return [num + ((num ^ (num+1)) >> 2) + 1 for num in numbers]
# 29.95ms, 25.3MB

비트 시프트 연산자는 '<<',  '>>' 를 사용한 연산자인데 비트단위에서 위치를 왼쪽이나 오른쪽으로 옮겨준다.

예를들어,

a = 8
b = a >> 1
print(b) # 4

b 값이 나오는 과정을 보면

1. 8 을 2진법으로 변경 : 1000
2. 1000 을 >>(오른쪽)으로 1만큼 스위치 : 0100
3. 0100 을 10진법으로 변경 : 4

이런식으로 작동한다.

 

또 위 식에 ^ (비트 XOR) 연산자가 있는데, 두 비트가 다를때 1, 같을때 0을 반환한다.

예를들어

• num = 2 일 때: (10 ^ 11) = 01
• num = 3 일 때: (11 ^ 100) = 111
• num = 4 일 때: (100 ^ 101) = 001
• num = 7 일 때: (111 ^ 1000) = 1111

이렇게 작동한다.

 

내가 생각한 로직과 비슷하지만 좀 더 컴퓨터 친화적인 풀이다. 비트를 직접 쓰는건 생각을 못했다.