[머신러닝] 선형 회귀와 경사 하강법

선형 회귀 (Linear Regression)

가설 (Hypothesis), 손실 / 비용 함수 (Cost / Loss function)

• 단순 선형회귀(1차 함수)를 가정하고 생각해보면 가설을 다음과 같이 세울 수 있다

  $$H(x) = Wx + b$$

  • W (Weight) 가중치 : 각 입력 특성에 대한 중요성을 결정
  • b (bias) 편향 : 실제 값과 예측 값 사이의 잔차를 보정

• 이렇게 만든 가설이 정답에 최대한 가까워지도록 해야한다 이때 주로 사용하는 것이 평균 제곱 오차(Mean Squared Error, MSE), 손실 함수라 한다

  $$MSE = 1/N * Σ (y_i - ŷ_i)^2$$

  • N은 데이터 포인트의 총 수
  • y_i는 i 번째 데이터 포인트의 실제 값
  • ŷ_i는 i 번째 데이터 포인트에 대한 모델의 예측값
  • 제곱이 들어가 있어서 예측과 실제 값 사이의 차이가 클수록 더 오차가 커진다

• $Cost = {{1\over N}\sum_{i=1}^{N}{(H(x_i) - y_i) ^ 2}}$ 로 표기하기도 함. 같은 수식

경사 하강법 (Gradient descent method)

https://towardsdatascience.com/using-machine-learning-to-predict-fitbit-sleep-scores-496a7d9ec48

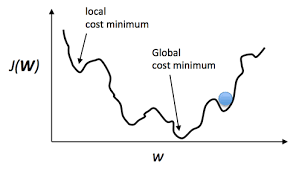
• 위 사진과 같이 손실함수가 있다고 가정하면 모델의 목표는 Cost를 최소화(Optimize)하는 것이다

• 점진적으로 하강해서 Cost가 최소값이 되는 Weight값을 찾는 것

• 그 점진적으로 움직이는 단위를 학습률(Learning rate) 라고 한다

학습률 (Learning rate)

https://medium.com/hackernoon/life-is-gradient-descent-880c60ac1be8

• 모델이 학습하는 동안 가중치를 얼마나 빠르게 갱신할지를 결정하는 매개변수

• 학습률이 너무 높으면, 손실 함수의 최소값을 지나칠 수 있어 모델의 성능이 떨어질 수 있음

https://medium.com/hackernoon/life-is-gradient-descent-880c60ac1be8

• 학습률이 너무 낮으면, 모델이 빠르게 학습하지 못하거나 지역 최소값(Local Minimum)에 갇힐 수 있음

https://regenerativetoday.com/logistic-regression-with-python-and-scikit-learn/

Uploaded by N2T