728x90
반응형
회귀 (Regression)
- 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링 하는 기법
- Y = W1 * X1 + W2 * X2 + W3 * X3 + … 이런 회귀식을 보면 Y는 종속변수, 즉 우리가 머신러닝을 통해 예측 할 가격이 되는 것이고, W1, W2, W3 은 독립 변수 값에 영향을 주는 회귀 계수(Regression coefficients) X1, X2, X3 은 독립변수가 된다.
- 머신러닝 회귀 예측은 주어진 피처(feature)와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾는 것이 목표
- 회귀는 회귀 계수의 선형/ 비선형 여부, 독립변수 개수, 종속 변수의 개수에 따라 여러가지 유형으로 나뉜다
| 독립변수 개수 | 회귀 계수의 결합 |
| 1개 : 단일 회귀 | 선형 |
| 여러 개 : 다중 회귀 | 비선형 |
선형회귀
- 실제 값과 예측값의 차이(오류의 제곱 값)를 최소화 하는 직선형 회귀선을 최적화 하는 방식
- 선형 회귀 모델은 규제(Regularization) 방법에 따라 별도의 유형으로 나뉨
- 규제(Regularization) : 일반적인 선형 회귀의 과적합 문제를 해결하기 위해 회귀 계수에 페널티 값을 적용하는 것
선형 회귀 모델들
- 일반 선형 회귀 : 예측값과 실제 값이 RRS(Residual sum of Squares)를 최소화 할 수 있도록 회귀 계수를 최적화하며, 규제를 적용하지 않은 모델
- 릿지 (Ridge) : 선형 회귀에 L2 규제를 적용한 회귀 모델. L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해 회귀 계수값을 더 작게 만드는 규제 모델
- 라쏘 (Lasso) : 선형 회귀에 L1 규제를 적용한 회귀 모델. L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것. L1 규제는 피처 선택 기능으로도 불린다
- 엘라스틱넷 (ElasticNet) : L2, L1 규제를 함께 결합한 모델. 주로 피처가 많은 데이터 세트에 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기 조정
- 로지스틱 회귀 (Logistic Regression) : 로지스틱 회귀는 회귀라는 이름이 붙어있지만, 분류에 사용되는 선형 모델. 매우 강력한 분류 알고리즘
분류 (Classification)
- 학습 데이터로 주어진 데이터의 피처와 레이블값(결정 값, 클래스 값)을 머신러닝 알고리즘으로 학습 후 모델 생성
- 학습된 모델에 새로운 데이터 값이 주어지면 미지의 레이블 값을 예측
- 기존 데이터가 어떤 레이블에 속하는지 패턴을 알고리즘으로 인지한 뒤에 새롭게 관측된 데이터에 대한 레이블을 판별
다양한 분류 머신러닝 알고리즘
- 나이브 베이즈 (Naive Bayes) :
- 베이즈(Bayes) 통계 : 이전의 경험과 현재의 증거를 토대로 어떤 사건의 확률을 추론하는 알고리즘
- 베이즈 통계와 생성 모델에 기반
- 로지스틱 회귀 (Logistic Regression) : 독립변수와 종속변수의 선형 관계성에 기반
- 결정 트리 (Decision Tree) : 데이터 균일도에 따른 규칙 기반
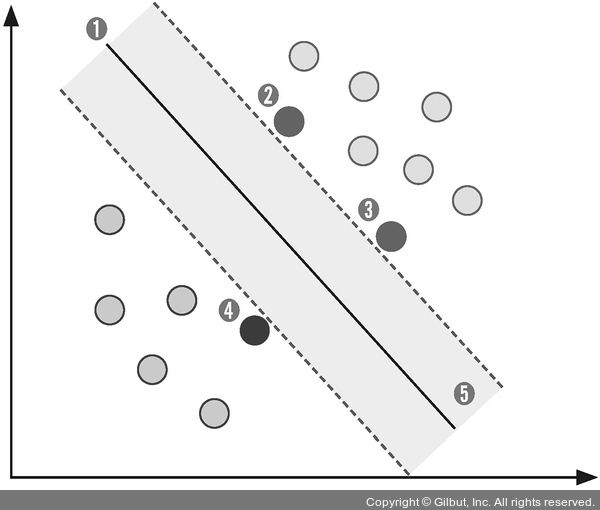
- 서포트 벡터 머신 (Support Vector Machine) : 개별 클래스 간의 최대 분류 마진을 효과적으로 찾아줌 아래 사진에서 1이 경계선, 2,3,4가 서포트 벡터, 5가 마진이다.
- 최소 근접 알고리즘 (Nearest Neighbor) : 근접 거리를 기준으로 하는 알고리즘
- 신경망 (Neural Network) : 심층 연결 기반
- 앙상블 (Ensemble) : 서로 다른/같은 머신러닝 알고리즘을 결합
Uploaded by N2T
728x90
반응형
